|
Optimal Form-Finding of Cable Systems |
 |
 |
 |
Dzierżanowski Grzegorz, Wójcik-Grząba Izabela, Optimal Form-Finding of Cable Systems, Archives of Civil Engineering, vol. 66, nr 3, 2020, ss. 305-321
DOI:10.24425/ace.2020.134399
online>>
Abstract
Tensile structures in general, achieve their load-carrying capability only after the process of initial form-finding. From the mechanical point of view, this process can be considered as a problem in statics. As cable systems are close siblings of trusses (cables, however, can carry tensile forces only), in our study we refer to equilibrium equation similar to those known from the theory of the latter. In particular, the paper regards designing pre-tensioned cable systems, with a goal to make them kinematically stable and such that the weight of so designed system is lowest possible. Unlike in typical topology optimization problems, our goal is not to optimize the structural layout against a particular applied load. However, our method uses much the same pattern. First, we formulate the variational problem of form-finding and next we describe the corresponding iterative numerical procedure for determining the optimum location of nodes of the cable system mesh. We base our study on the concept of force density which is a ratio of an axial force in cable segment to its length. |
|
Recovery of the Auxetic Microstructures Appearing in the Least Compliant Continuum Two-Dimensional Bodies |
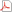 |
 |
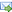 |
Sławomir Czarnecki, Tomasz Łukasiak, Recovery of the Auxetic Microstructures Appearing in the Least Compliant Continuum Two-Dimensional Bodies, Physica Status Solidi (b) 1900676, 2020 (16 stron)
Available on line(https://doi.org/10.1002/pssb.201900676)>>
Abstract
The article discusses the 2D problem of manufacturability of the minimum compliance designs of the structural elements made of inhomogeneous materials of local isotropic or square symmetry properties. The available isotropic material design (IMD) and cubic material design (CMD) methods deliver the optimal distribution of the elastic moduli within the design domain. Within the 2D setting, the cubic symmetry reduces to the symmetry of a square. The varying underlying microstructures corresponding to the optimal designs are recovered by matching the values of the optimal moduli with the values of the effective moduli of the representative volume elements (RVEs) computed by the asymptotic homogenization method for periodic media. The shape of the RVE and its internal symmetries are properly selected providing assumed isotropy or symmetry of a square of the homogenized constitutive tensor. The microstructure topology is described by parametric description of single (or several) fibers in RVE. The periodicity of the structure and the final topology of the material within RVE is ensured by multiplication of a single fiber in accordance with the symmetries adopted for RVE. The ability to model an auxetic behavior within the subdomains where the optimal Poisson's ratio assumes negative values is shown. |
|
Michell structures within L-shaped domains |
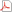 |
 |
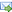 |
K. Bołbotowski, T. Lewiński, T. Sokół, Michell structures within L-shaped domains, Computer Assisted Methods in Engineering and Science (CAMES),2020
on line: https://cames.ippt.pan.pl/index.php/cames/article/view/281
DOI: https://doi.org/10.24423/cames.281.
Abstract
By recalling the main mathematical results concerning the theory of Michell structures, the present paper puts forward an interpretation of the selected numerical methods for constructing their approximants, that is, trusses with a large number of nodes. The efficiency of one of these methods: the ground structure method in its adaptive version is shown in the context of the L-shaped design domain problem. A large family of highly accurate truss approximants corresponding to the point loads acting at selected vertices is constructed and discussed. |
|
Optimal archgrids: a variational setting |
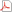 |
 |
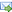 |
R. Czubacki, T. Lewiński, Optimal archgrids: a variational setting, Structural and Multidisciplinary Optimization 2020,
https://doi.org/10.1007/s00158-020-02562-y
Abstract
The paper deals with the variational setting of the optimal archgrid construction. The archgrids, discovered by William Prager and George Rozvany in 1970s, are viewed here as tension-free and bending-free, uniformly stressed grid-shells forming vaults unevenly supported along the closed contour of the basis domain. The optimal archgrids are characterized by the least volume. (...)
on-line >>
|
|
Ś.P. Krzysztof Zbigniew Hetmański (1958-2020)-wspomnienie |
 |
 |
 |
Krzysztof Hetmański urodził się 24 października 1958 r. Obdarzony wybitną inteligencją lecz naznaczony przez los słabym zdrowiem, w czasie studiów (lata 1976-1980) na Wydziale Inżynierii Lądowej wielokrotnie chorował. Ze względu na bardzo zły stan zdrowia przerwał studia na jesieni 1980 r. na początku semestru dyplomowego a następnie kilka razy wznawiał a potem znów rezygnował. Mimo nękających Go chorób Krzysztof uzyskał w 1988 r. stopień magistra inżyniera budownictwa (specjalność Konstrukcje Budowlane i Inżynierskie, specjalizacja: Teoria Konstrukcji) na podstawie pracy magisterskiej pt.:
Uściślony trójkątny element skończony płyty o średniej grubości. Promotorem był Andrzej Gomuliński (wówczas docent PW) a konsultantem Wojciech Gilewski (wówczas adiunkt PW). Recenzję opracował prof. Zbigniew Kączkowski. W pracy tej Krzysztof znalazł błąd merytoryczny w budowie elementu trójkątnego płytowego zaproponowanego przez prof. Kączkowskiego i zaproponował własną wersję tego elementu. Niestety, wyniki tej pracy nie zostały opublikowane.
|
|
Więcej…
|
|
Higher order weighted Sobolev spaces on the real line for strongly degenerate weights. Application to variational problems in elasticity of beams |
 |
 |
 |
Karol Bołbotowski, Higher order weighted Sobolev spaces on the real line for strongly degenerate weights. Application to variational problems in elasticity of beams,
Journal of Mathematical Analysis and Applications, vol 488, 2020, str 58,
|
|
|