|
A note on optimal design of multiphase elastic structures |
 |
 |
 |
 A note on optimal design of multiphase elastic structures
N. Briggs, A. Cherkaev, G. Dzierżanowski
Structural and Multidisciplinary Optimization: Volume 51, Issue 3 (2015), Page 749-755,
Read online>>
The paper describes the first exact results in optimal design of three-phase elastic structures. Two isotropic materials, the "strong" and the "weak" one, are laid out with void in a given two-dimensional domain so that the compliance plus weight of a structure is minimized. As in the classical two-phase problem, the optimal layout of three phases is also determined on two levels: macro- and microscopic. On the macrolevel, the design domain is divided into several subdomains. Some are filled with pure phases, and others with their mixtures (composites). The main aim of the paper is to discuss the non-uniqueness of the optimal macroscopic multiphase distribution. This phenomenon does not occur in the two-phase problem, and in the three-phase design it arises only when the moduli of material isotropy of "strong" and "weak" phases are in certain relation. |
|
Optymalizacja topologiczna konstrukcji inżynierskich. |
|
|
|
Projekt badawczy Narodowego Centrum Nauki pt.:
Optymalizacja topologiczna konstrukcji inżynierskich. Ujęcie syntetyzujące metody: projektowania anizotropii z wolnego wyboru, projektowania materiałów niejednorodnych oraz metodę siatek typu Michella,
Kierownik: prof. dr hab. inż. Tomasz Lewiński,
Politechnika Warszawska; Wydział Inżynierii Lądowej,
środki przyznane: 772 040 zł,
zajął 5. miejsce spośród 188 projektów złożonych w ramach konkursu: OPUS, Panel ST 8 (data ogłoszenia: 16 IX 2013 r.). Do drugiego etapu zakwalifikowano 47 wniosków; do finansowania skierowano 32 wnioski.
Projekt ten będzie wykonywany w ramach umowy:
UMO-2013/11/B/ST8/04436
zawartej w dniu 15 lipca 2014 r. pomiędzy
NCN a Politechniką Warszawską.
Nr projektu: 2013/11/B/ST8/04436
Okres realizacji: 15.07.2014-14.07. 2017, przedłużony aneksem do 14.12.2017.
|
|
Read more...
|
|
Informatyzacja projektowania budowlanego |
|
|
|
Informatyzacja projektowania budowlanego, Zbigniew Kacprzyk, Konferencja Budmika 2014, Poznań, 23-25 kwietnia 2014 roku
Wykład „Informatyzacja projektowania budowlanego" ma na celu przybliżenie współczesnych narzędzi pracy projektanta budowlanego na tle przełomowych odkryć w informatyce , w mechanice obliczeniowej i modelowaniu geometrycznym.
Z całego obszaru „informatyzacji projektowania" dokładniej omówię informatyzację obliczeń inżynierskich oraz informatyzację modelowania geometrycznego. Na końcu zajmę się problemami integracji oprogramowania – czyli problemami wymiany danych.
Prezentacja>> 10.56 MB |
|
A stress-based formulation of the free material design problem with the trace constraint and multiple load conditions |
|
|
|
A stress-based formulation of the free material design problem with the trace constraint and multiple load conditions. 
S. Czarnecki, T.Lewiński,
Structural and Multidisciplinary Optimization, 2014 in press
Read online>>
The paper deals with minimization of the weighted sum of compliances related to the load cases applied non-simultaneously. The design variables are all components of the Hooke tensor, subject to the isoperimetric condition bounding the integral of the sum of the Kelvin moduli. This free material design problem is reduced to an equilibrium problem – in two formulations – of an effective body with locking. The stress-based formulation reduces to minimization of an integral of a certain norm of stress fields over the stress fields which equilibrate the given loads. The equivalent displacement-based formulation involves a locking locus defined by using a norm being dual to the previous one. The optimal Hooke tensor is determined by using the stress fields solving the auxiliary locking problem. To make the optimal Hooke tensor positive definite one should consider at least 3 load conditions in the 2D case and not less than 6 load conditions in the 3D case.
|
|
Recovery of two-phase microstructures of planar isotropic elastic composites |
|
|
|
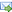10th World Congress on Structural and Multidisciplinary Optimization
May 19-24,2013, Orlando,Florida, USA
Recovery of two-phase microstructures of planar isotropic elastic composites
Read onlie>>
Abstract
The isotropic elastic mixtures composed of two isotropic materials of the bulk moduli and shear moduli are characterized by the effective bulk and shear moduli. In the planar problems the theoretically
admissible pairs, for given volume fraction ρ 0 of material, lie within a rectangular domain of vertices determined by the Hashin-Shtrikman bounds. The tightest bounds in 2D known up till now are due to
Cherkaev and Gibiansky (CG). The microstructures corresponding to the interior of the CG area can be of arbitrary rank, in the meaning of the hierarchical homogenization. In the present paper a family of composites is constructed of the underlying microstructures of rank 1. The consideration is confined to the microstructures possessing rotational symmetry of angle 1200. To find the effective moduli the homogenization method is used: the local basic cell problems are set on a cell Y of the shape of a hexagonal domain. The periodicity conditions refer to the opposite sides of Y. Such a non-conventional basic cell choice generates automatically the family of isotropic mixtures. The subsequent points are found by solving the inverse homogenization problems with the isoperimetric condition expressing the amounts of both the materials within the cell. The isotropy conditions, usually explicitly introduced into the inverse homogenization formulation, do not appear, as being fulfilled by the microstructure construction. The method put forward makes it possible to localize each admissible pair by appropriate choice of the layout of both the constituents within the repetitive sub-domain of Y.
Keywords: isotropic composites, inverse homogenization, recovery of microstructures. |
|
Two-phase isotropic composites with prescribed bulk and shear moduli |
|
|
|
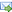Two-phase isotropic composites with prescribed bulk and shear moduli.
T. Łukasiak
Read online>>
ABSTRACT: The paper deals with the inverse homogenization problem: to reconstruct the layout of two elastic and isotropic materials given by bulk and shear moduli within a hexagonal (2D) pe-
riodicity cell, corresponding to the predefined values of the bulk and shear moduli, of the effective isotropic composite and to the given isoperimetric condition concerning the volume fractions. The effective
isotropic moduli are computed according to the homogenization algorithm, with using appropriate Finite Elements (FE) techniques along with periodicity assumptions. The inverse problem thus formulated can be ef-
fectively solved numerically by the Sequential Linear Programming (SLP) method. The isotropy conditions, usually explicitly introduced into the inverse homogenization formulation, do not appear in the algorithm, as
being fulfilled by the microstructure construconstruction. The rotational symmetry of angle 120o of the resulting representative volume element is assumed. |
|
|
